我們來回顧一下正弦波的定義:
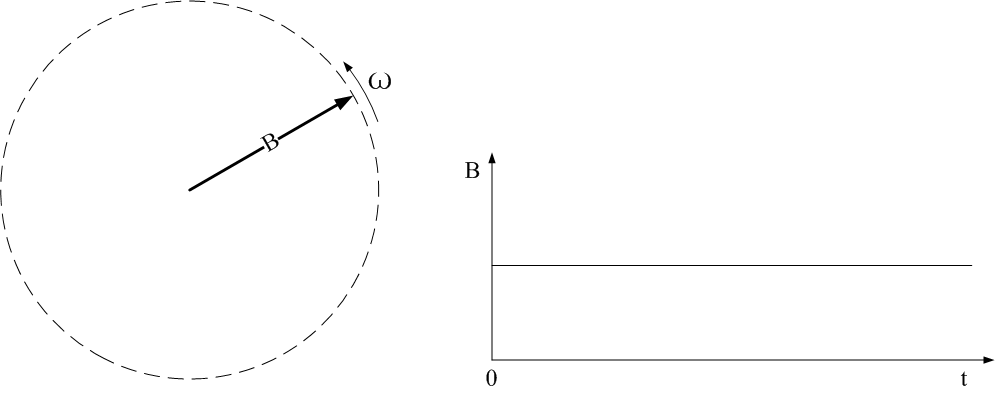
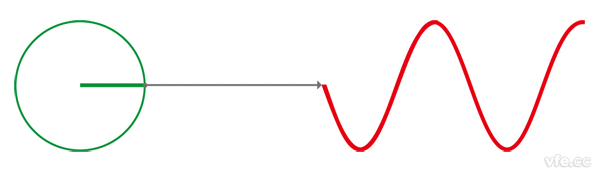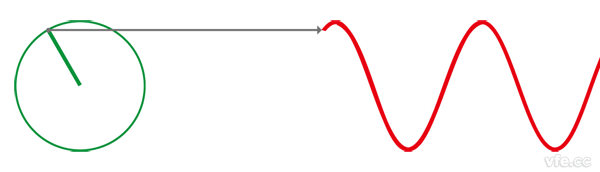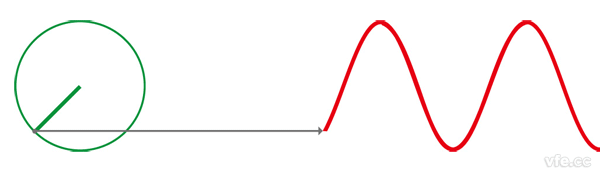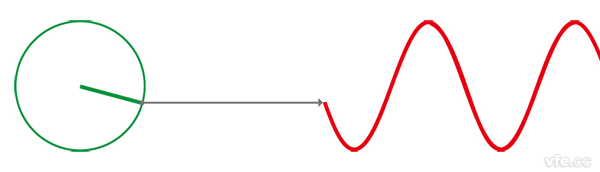
如下圖所示:正弦波是圓周運動在一條直線上(圖中為平面坐標系的y軸)的投影。
圖2、正弦波的定義
上述動畫清晰的描述了正弦波與圓周運動有內在聯系。顯然,用圓形旋轉磁場可以產生正弦波。具體方法是將一個繞組擺放在圓形旋轉磁場中,繞組將感應出正弦波電壓,這就是同步發電機的工作原理。同步發電機轉子通過直流電流,產生的是幅值恒定的磁場,轉子旋轉,產生圓形旋轉磁場,該磁場切割定子繞組,定子繞組感應出正弦電壓,繞組形成閉合回路,即可產生正弦波電流。
于是,我們設想,可不可以反過來用正弦波電流來產生圓形旋轉磁場呢?
正弦波電流通過一個繞組,產生的是正弦磁場,該磁場幅值按照正弦規律變化,而方向始終在繞組軸線上。
根據矢量合成的道理,我們知道,兩個不同方向(夾角不是0°或180°)的矢量,可以合成一個方向與原矢量均不相同的新矢量。改變兩個矢量的方向或幅值,均可改變合成矢量的方向。
那么,用兩個固定方向(夾角不是0°或180°)的正弦波磁場,能不能合成圓形旋轉磁場呢?
答案是肯定的!
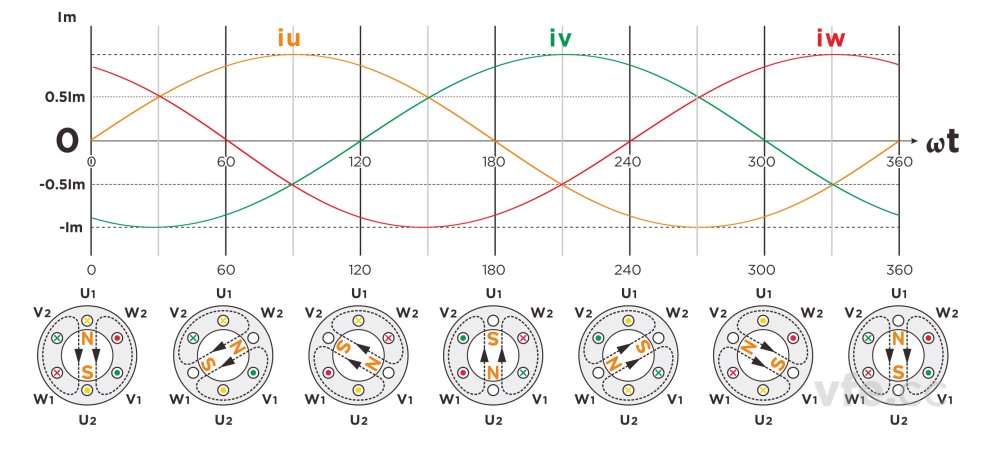
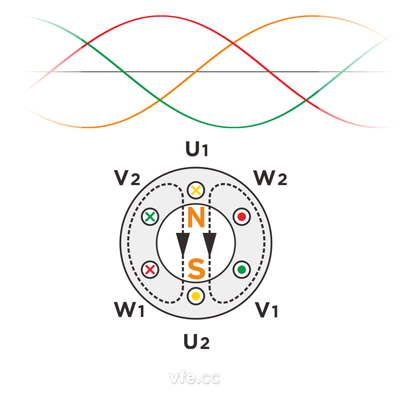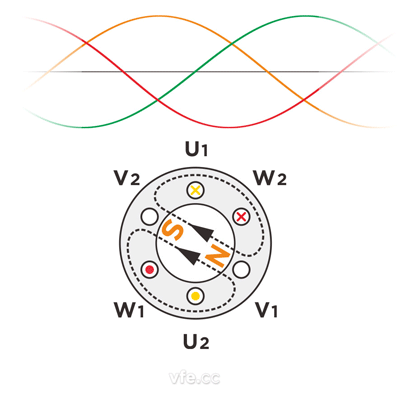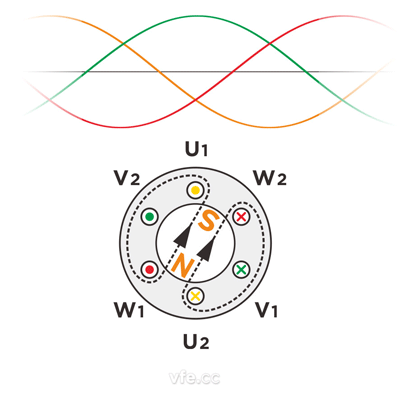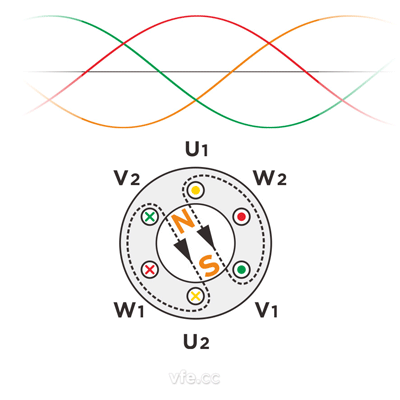
如圖3所示,空間位置依次相差120°的三個相同繞組,施加三相對稱正弦電壓后,分別在各自軸線上的產生正弦磁場。
圖3、圓形旋轉磁場的產生過程
在t0、t1、t2、t3、t4、t5時刻,三個磁場的合成矢量的角度分別為30°、90°、150°、210°、270°、330°。
將上述時刻連動起來,就得到下述旋轉磁場的動畫:
圖4、圓形旋轉磁場動畫
圖3和圖4從幾個典型角度粗略描述了圓形旋轉磁場的產生過程。接下來,我們從理論角度對其進行證明。
首先,一個正弦磁場可以分解為兩個幅值為其1/2,方向相反的旋轉磁場。證明如下:
假設正弦磁場的表達式為:
B=Bmsin(ωt)(1)
該磁場是一個矢量,其方向為y軸的正向,其幅值隨時間按正弦規律變化。
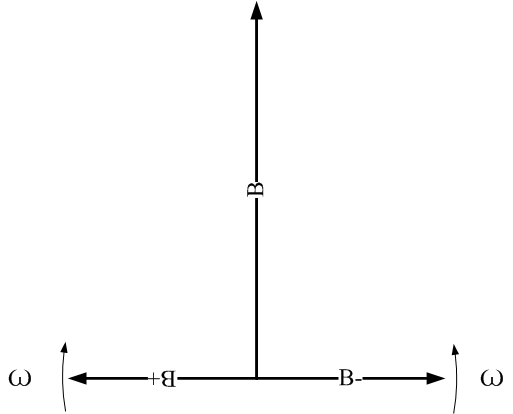
如圖5所示,定義兩個幅值均為0.5Bm的旋轉磁場B+和B-:
圖5、旋轉磁場定義
兩個旋轉磁場對稱分布在y軸兩側,其中B-的初始角度為0°(B順時針旋轉90°),以角速度ω逆時針旋轉;B+的初始角度為180°(B逆時針旋轉90°),以角速度ω順時針旋轉。
在時刻t,兩者在x軸上的合成磁場為:
Bx=0.5Bmcos(ωt)+0.5 Bmcos(π-ωt)= 0.5Bmcos(ωt)- 0.5Bmcos(ωt)=0
兩者在y軸上的合成磁場為:
By=0.5Bmsin(ωt)+0.5 Bmsin(π-ωt)= Bmsin(ωt)
現在我們來合成圓形旋轉磁場。
其次,使空間分布角度依次相差120°的三個繞組均產生式1所述的正弦磁場。
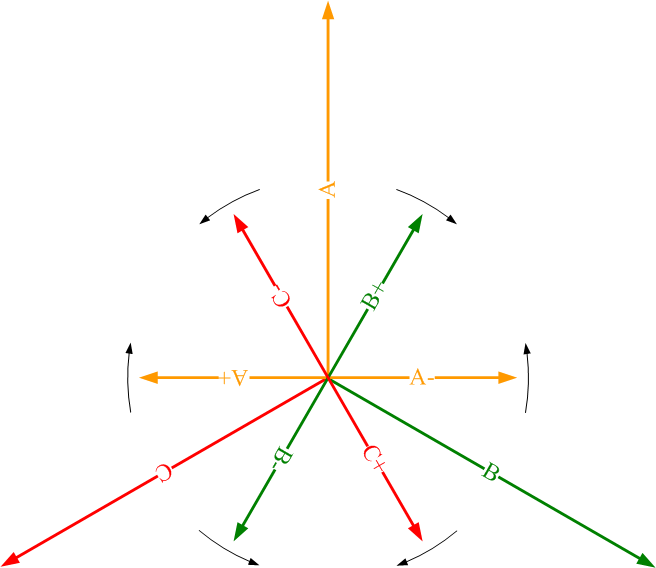
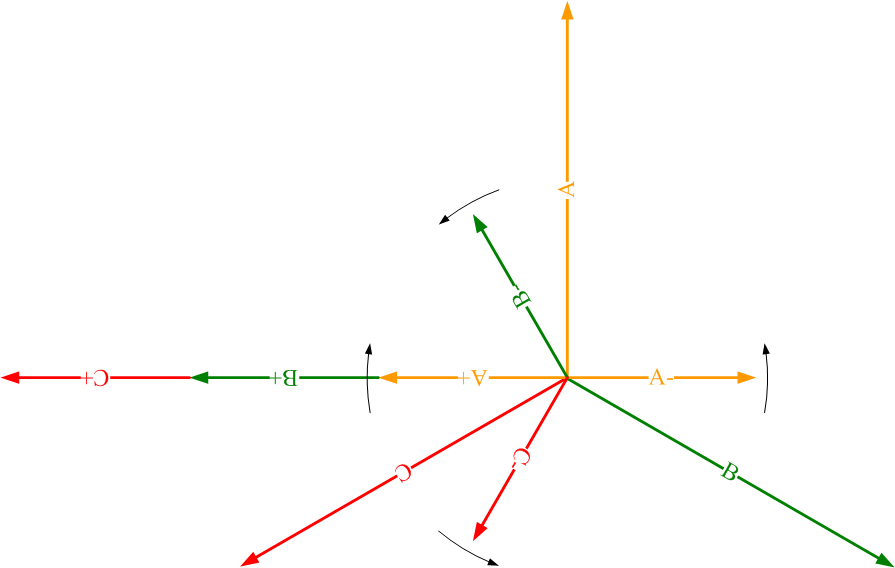
如圖6所示,將A、B、C三個繞組分別分解為兩個幅值相等,旋轉方向相反的旋轉磁場,得到A+、A-、B+、B-、C+、C-六個旋轉磁場。
圖6、旋轉磁場分解
注:(A、B、C為正弦磁場,圖中方向為繞組軸線方向,而非相位角,為固定角度。A+、A-、B+、B-、C+、C-為旋轉磁場,方向為旋轉磁場的初始角度,隨時間變化而變化。)
最后,由于實際三相繞組存在120°的相位差,表達式如下:
BA=Bmsin(ωt)
BB=Bm sin(ωt-120°)
BC=Bm sin(ωt-240°)
因此,圖6的B-、B+、C-、C+應當作如下變換:
由于B相滯后A相120°,B-和B+應倒轉120°
即:B-順時針旋轉120°;B+逆時針旋轉120°
由于C相滯后A相240°,C-和C+應倒轉240°
即:C-順時針旋轉240°;C+逆時針旋轉240°
變換結果如圖7所示。
圖7、旋轉磁場合成
顯然,三個逆時針矢量相互抵消,合成磁場為零,而三個順時針矢量方向一致,合成磁場幅值為三個磁場的總和1.5Bm。合成磁場按照順時針方向旋轉,即:旋轉磁場的方向與電流的相序相同。